AABB

발생

충돌 검출에 대해 알아보다 알게된 용어이다.

AABB란 Axis-Aligned Bounding Box 의 단축어다.
한국어로는 축 경계 정렬 상자 라고 부를 수 있다.

AABB는 물체의 충돌 범위를 정하는 방법 중 하나이며 가장 단순한 방법이라고 할 수 있다.

AABB는 물체를 감싸는 좌표축에 정렬된 직육면체이다.

AABB는 항상 모든 면이 좌표축에 평행하고 회전하지 않는다. 또한 항상 축에 맞춰진 직사각형 모양이다.

아래는 AABB의 2D 예시 이미지이다.

AABB 예시 이미지

위 사진만 보면 이해가 힘드니 아래 예시 이미지들을 본다면 이해가 더 쉬울것이다.

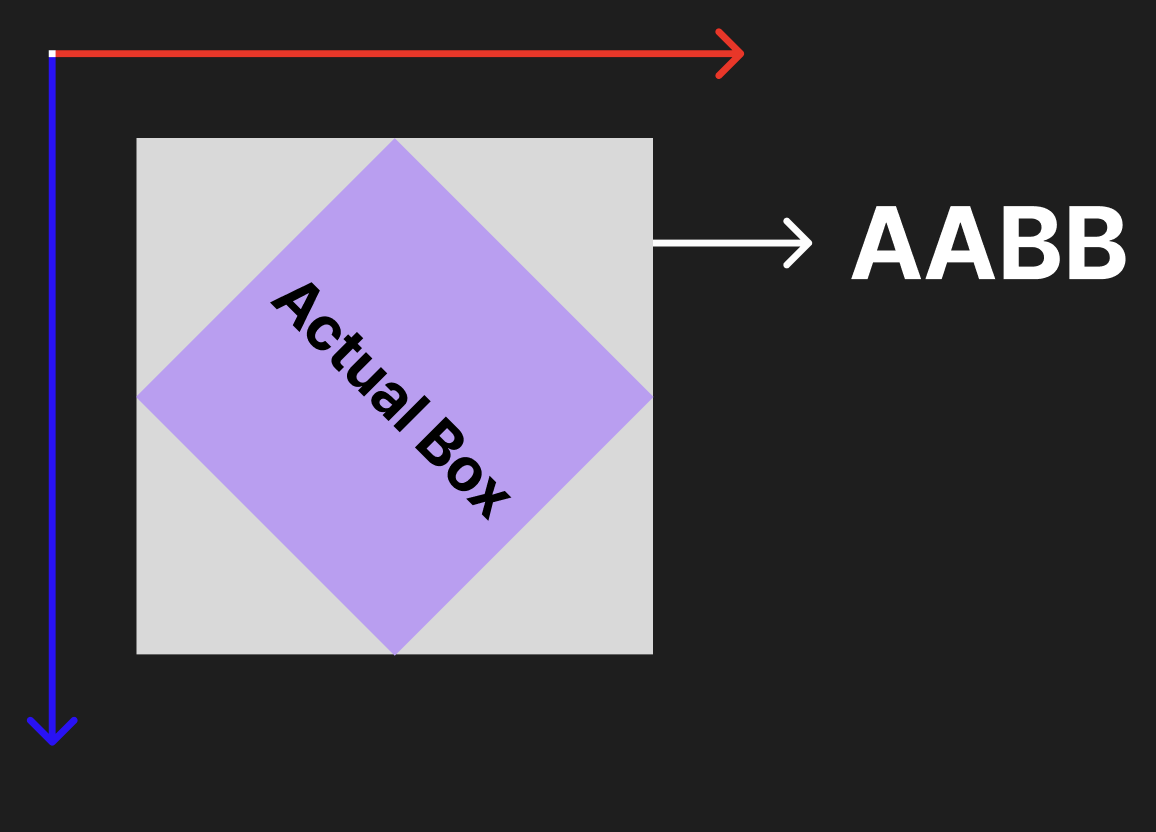
AABB 예시 2

요소의 모양과 상관 없이 AABB는 좌표축에 모든 면이 평행한 직사각형으로 만들어진다. 이는 후술할 AABB의 단점과 직결되는 특징이기도 하다.

AABB는 보통 두 점으로 정의한다.

3차원에서 AABB의 경계는 아래와 같다.

$x \in [x_{min}, x_{max}],\quad y \in [y_{min}, y_{max}],\quad z \in [z_{min}, z_{max}]$

두 점만 안다면 AABB의 크기, 중심, 절반 크기 등을 알 수 있다.

$center = \frac{min + max}{2}, \quad halfSize = \frac{max - min}{2}$

AABB는 복잡한 물체를 단순한 상자로 근사하여 충돌 검출을 빠르게 수행하기 위해 사용된다.

예시로 매우 복잡한 모양의 물체를 단순화 하지 않고 모든 면들에 대해 충돌을 검출하려면 수백-수천개의 면을 모두 검사해야 하므로 연산량이 매우 많아진다. 하지만 AABB를 활용한다면 아주 단순한 비교만드로도 충돌 판단을 아주 간단한 연산으로 처리 할 수 있다.

2차원에서의 A,B의 AABB 충돌 조건은 아래와 같다.

$A.x_{min} < B.x_{max} \quad \text{and} \quad A.x_{max} > B.x_{min}$
$A.y_{min} < B.y_{max} \quad \text{and} \quad A.y_{max} > B.y_{min}$

위 조건이 모두 참이면 두 상자는 겹친 상태라는 뜻이다.

이와 같이 단순한 4개의 비교 연산만으로 충돌 여부를 파악 할 수 있다.

AABB의 장점은 빠르고, 단순하다는 점이다.

이런 장점에서 기인하는 단점이 존재한다 단점으로는 물체가 회전을 하거나 복잡한 형태를 가지면 정확도가 떨어진다는 것이다.

AABB 예시 이미지 3
출처 : https://blog.csdn.net/qq_22822335/article/details/50930437

위 사진과 같이 물체가 회전을 한다면 AABB는 이 물체의 최대, 최소 지점 만으로 박스를 만들기 때문에 빈 공간이 많이 생기게 된다 이는 곧 충돌 판정의 정확도 하락을 의미한다 이는 물체의 복잡한 형태에도 그대로 적용된다.

AABB는 물리 엔진의 충돌 검출 단계인 Broad Phase에 주로 쓰인다.

충돌 구현을 이해함에 있어 반드시 알아야 할 용어였다.

Day-45

tech